Splines (1ª parte)

Además de los comandos SPLINE y EDITSPLINE (SPLINEDIT), que permiten representar y modificar curvas B-spline, AutoCAD proporciona otros muchos comandos en los que este tipo de curvas interviene de forma directa o indirecta. La opción Spline del comando EDITPOL (PEDIT), por ejemplo, permite transformar una polilínea en una aproximación a una curva B-spline cuadrática o cúbica. La opción Tipo (Type) del comando BOCETO (SKETCH) ofrece la posibilidad de utilizar objetos de tipo spline para el trazado. Y también podríamos citar los comandos DIRECTRIZ (LEADER) o HELICE (HELIX), entre otros.

Para utilizar este tipo de curvas con un mínimo de conocimiento es preciso entender sus propiedades gráficas y geométricas. Sin en esta base, la utilización de curvas B-splines en un dibujo difícilmente puede considerarse algo más que puro entretenimiento. La práctica totalidad de los tratados de AutoCAD e incluso la propia ayuda en línea que proporciona el programa resultan de muy escasa utilidad en este sentido.

Sin entrar en el soporte matemático, que sobrepasa con mucho nuestros objetivos, con este artículo iniciamos una serie donde expondremos las características y propiedades de las curvas B-splines que, a nuestro entender, son esenciales para el diseñador.


Un poco de historia. Curvas de Bezier

Las curvas B-splines se engloban dentro de lo que se conoce generalmente como curvas de diseño, cuyo desarrollo práctico se inició en la década de los 60 debido de las exigencias estéticas y funcionales que se planteaban en el diseño de carrocerías (automóviles, aviones o barcos) y que hacían necesaria la utilización de formas geométricas no tradicionales. En el pasado, el diseño de estas superficies era completamente artesanal. Las curvas se trazaban sobre planchas metálicas con la ayuda de junquillos flexibles, denominados splines, que se fijaban en la mesa de trazado mediante unas piezas pesadas conocidas con el nombre de ducks (patos, en inglés).

Uno de los primeros métodos modernos de modelado de curvas fue desarrollado de forma simultánea por los ingenieros Paul de Casteljau en Citroën y Pierre Bezier en Renault. Las curvas obtenidas por este método han pasado a la posteridad como curvas de Bezier, debido a que este último publicó sus investigaciones en 1966, lo que no hizo de Casteljau.

Las curvas de Bezier se calculan a partir de una poligonal de n vértices, que recibe el nombre de polígono de control. La expresión matemática de las curvas de Bezier es la siguiente:

donde P representa cada uno de los puntos de la curva, Vi los vértices del polígono de control y u es un parámetro que toma valores incrementales desde 0 hasta 1 a lo largo de la curva. El primer punto de la curva se obtiene cuando u = 0 y el último cuando u = 1.

Sin entrar en demasiadas profundidades matemáticas, en la expresión anterior se pueden observar dos particularidades que, como veremos más adelante, tendrán una importancia decisiva en el desarrollo de las curvas B-splines. La primera es que en el cálculo de cada punto de la curva intervienen todos los vértices, Vi , del polígono de control. Y la segunda es que el grado que alcanza la ecuación depende directamente del número de vértices, n, del citado polígono.

Las propiedades más relevantes desde un punto de vista geométrico y gráfico de las curvas de Bezier son las siguientes:

• Comienzan y terminan en los vértices extremos del polígono de control y son tangentes a los lados extremos.
• Están contenidas en la envolvente convexa de su polígono de control, es decir, siempre son interiores al menor polígono convexo que contiene a todos los vértices del polígono de control.
• Una recta arbitraria no corta a la curva en más puntos que a su polígono de control.
• Si se invierte el orden de los vértices del polígono cambia la parametrización de la curva, pero geométricamente sigue siendo la misma.
• La curva puede ser abierta o cerrada y puede cortarse a sí misma. Para que la curva se cierre basta que el primer vértice y el último coincidan. Para que haya continuidad de la tangente en el cierre, el último lado del polígono debe estar en la misma recta soporte que el primero.

La figura siguiente muestra tres ejemplos de curvas de Bezier, junto con su correspondiente polígono de control, donde se pueden observar algunas de las propiedades citadas.

A pesar de que las curvas de Bezier constituyeron un avance importantísimo en el Diseño Asistido por Ordenador, el método de cálculo que utilizan tiene dos serios inconvenientes, que ya hemos avanzado. El primero es que todos los vértices del polígono de control intervienen en el cálculo de cada uno de los puntos de la curva. Por lo tanto, cualquier cambio, por pequeño que sea, en alguno de los vértices del polígono afecta a toda la curva en su conjunto. En términos técnicos, esto se expresa diciendo que las curvas de Bezier carecen de control local. El segundo inconveniente es que el grado de la ecuación que se utiliza en el cálculo está directamente relacionado con el número de vértices del polígono de control. Así, por ejemplo, si el polígono tiene 3 vértices la ecuación es de segundo grado; si tiene 4 vértices la ecuación es de tercer grado y, así, sucesivamente. En consecuencia, al aumentar el número de vértices del polígono de control se aumenta considerablemente la complejidad del cálculo.


Curvas B-splines

Las curvas B-splines resuelve ambos problemas utilizando un fundamento matemático similar al de las curvas de Bezier y tienen las mismas propiedades que hemos citado. La diferencia entre unas y otras está en que las curvas B-splines se calculan por tramos, asegurando la continuidad de la tangente entre cada dos tramos consecutivos, lo que da como resultado una curva continua.

Todos los tramos de la curva se calculan en función del mismo número de vértices consecutivos, pero este número de vértices, que recibe el nombre de orden de la curva, es elegido a voluntad por el diseñador. El grado de la ecuación utilizada en el cálculo de cada tramo es inferior en una unidad al orden de la curva. Así, por ejemplo, en una curva B-spline de orden 3, cada tramo se calcula con una ecuación de segundo grado en la que intervienen 3 vértices consecutivos del polígono de control. Los vértices primero, segundo y tercero dan lugar al primer tramo de la curva; los vértices segundo, tercero y cuarto al segundo tramo y, así, sucesivamente, hasta llegar al último tramo, que se obtendría a partir de los vértices antepenúltimo, penúltimo y último.

De lo dicho en el párrafo anterior, podemos extraer algunas consecuencias prácticas interesantes de cara a la utilización del comando SPLINE o de la opción Spline del comando EDITPOL (PEDIT).

• Cuando se dibuja una curva B-spline de grado 2 (ecuación de segundo grado), AutoCAD utiliza tres vértices consecutivos del polígono de control para calcular cada tramo de la curva y el número de tramos es igual al número de vértices del polígono de control menos dos. La figura siguiente muestra un ejemplo de curva B-spline cuadrática obtenida a partir de un polígono de control de 7 vértices donde se han marcado con puntos los extremos de los 5 tramos que forman la curva.

• Cuando se dibuja una curva B-spline de grado 3 (ecuación de tercer grado), AutoCAD calcula cada tramo de la curva utilizando cuatro vértices consecutivos del polígono de control. Por lo tanto, el número de tramos de la curva será igual al número de vértices del polígono de control menos tres. En la figura siguiente está representado el mismo polígono del ejemplo anterior, pero la curva que se ha dibujado es una B-spline cúbica. Obsérvese que, en este caso, la curva sólo está compuesta por cuatro tramos.

Con respecto a esta segunda consecuencia, cabe plantearse la siguiente pregunta: ¿Cómo opera AutoCAD para obtener una curva B-spline cúbica a partir de un polígono de control de 3 vértices, si para definir un solo tramo de la curva son necesarios 4 vértices? Pues de una forma muy sencilla: ignorando por completo el grado y representando una curva B-spline cuadrática. Esto significa que el comando SPLINE exige que el número de vértices del polígono de control exceda, al menos, en una unidad al grado que se haya establecido para la curva. De lo contrario, el grado de la curva resultante será igual al número de vértices del polígono de control menos uno.

Ahora que sabemos el número de vértices del polígono de control que intervienen en cada tramo de la curva, podemos deducir otra propiedad interesante:

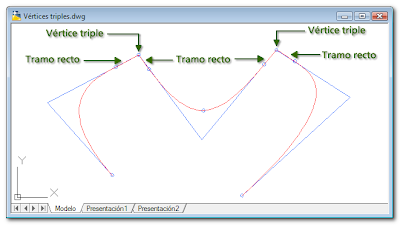
• En una curva B-spline cuadrática, cuando dos vértices consecutivos del polígono de control son coincidentes, la curva pasa por ellos. Por tanto, el tramo de la curva en el que intervienen ambos vértices será un segmento recto. Lo mismo sucede en una curva B-spline cúbica cuando son coincidentes tres vértices consecutivos del polígono de control (como en la figura siguiente) y, así, sucesivamente.

Antes de terminar conviene recordar que el comando SPLINE dibuja la curva por defecto a partir de sus puntos de paso, lo que exige hacer uso de la opción Método (Method) y la subopción VC (CV) si lo que se pretende es representar la curva a partir de su polígono de control. Una vez efectuado este ajuste, la opción Grado (Degree) permite definir el grado de la ecuación utilizada para calcular la curva. Ambos parámetros se pueden establecer también por medio de las variables de sistema SPLMETHOD y SPLDEGREE. Esta última variable admite valores comprendidos entre 1 y 10. El valor 1 determina la utilización de una ecuación de primer grado para dibujar la curva, por lo que el resultado en el dibujo es una simple sucesión de segmentos rectos.

Ir a 2ª parte ...